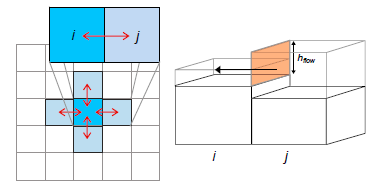
In the present work, the proposed CoastFLOOD module for the simulation of extended coastal inundation due to storm surges is based on the classic “raster-based storage cell” concept, structure and numerical approach of the well-established LISFLOOD-FP model (Bates & De Roo, 2000; Bates et al., 2005; 2010; 2013; Seenath et al., 2016). In our case the sea level elevation on the shoreline of the coastal zone interacts with the coastal floodplain via a Manning-type flow equation in 2-D formulation, allowing seawater to inundate and freely return flow between adjacent computational cells of the grid representing the floodplain terrain.

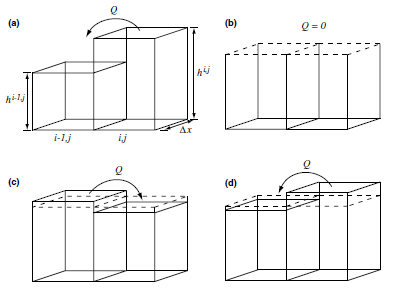
The CoastFLOOD module is attached to MeCSS for the simulation of coastal flooding due to storm surges (Makris et al., 2020; 2021; Skoulikaris et al., 2020). CoastFLOOD practically solves the decoupled 1-D flow equations in zonal and meridional directions for expanded inundation events at each front of an orthogonal 2-D grid cell, in order to provide a 2-D solution in each horizontal direction (on the x- and y-direction, respectively) of the flow (Bates et al., 2010). Based on the approach of Bates et al. (2005), the continuity equation corresponds to the mass conservation principle for the calculation of local water depth (free-surface height) in each gridded cell. The module is led to flow route estimation by a simplistic quad-tree search algorithm for upstream cells and a dry/wet cell storage code, based on the difference of hydraulic head between neighboring cells. The flow rate is derived by a Manning’s law approach using the water surface elevation above land level incorporating bottom friction.

CoastFLOOD’s input consists of the boundary conditions of the MeCSS model implementation, namely SSH and depth-averaged, zonal and meridional, sea currents u and v on the coastal front. Along the coastline the required topographic and hydrographic parameters are the local water level (defined by the difference of SSH over land elevation z), water velocity (depth-averaged coastal current) on the boundary, the cell dimensions, Manning’s coefficient n, and the floodplain’s bed elevation z. The latter gives the bed slope in every direction of the flow over the floodplain DEM’s nodes. Negative and positive gradients (upward and downward trends) of the bed elevation profiles in x- and y-directions are calculated explicitly through the numerical scanning of the solution and integration procedure.  

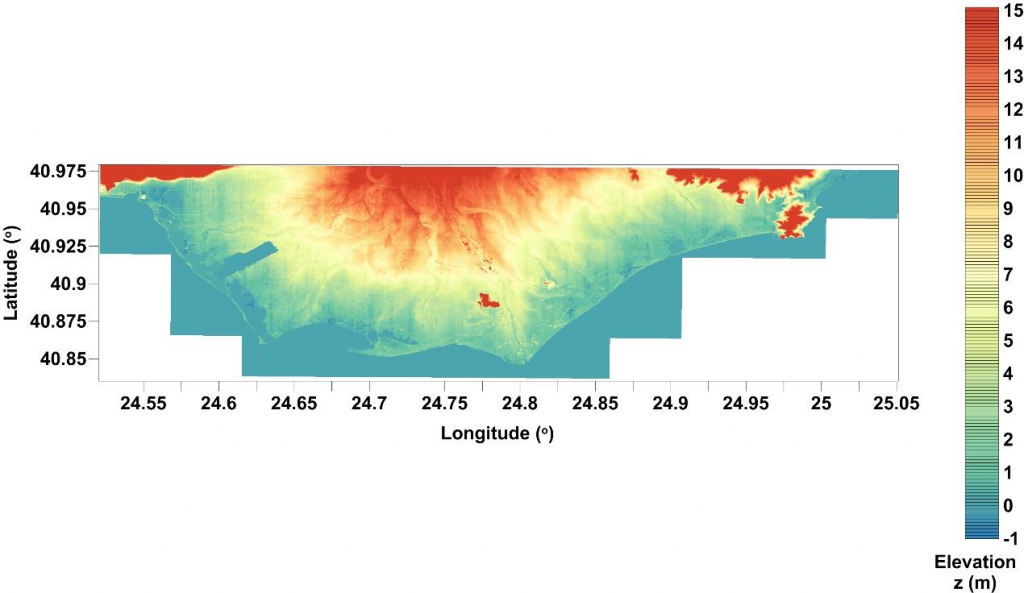
CoastFLOOD was run on a high-resolution computational field, which consists of nearly 28∙10 6 cells, applying a classic wet/dry storage cell algorithm for the assignment of flood fronts over steep slopes. The computational field’s DEM input data of CoastFLOOD were derived via post-processing raster images of the Hellenic Cadastre’s (https://www.ktimatologio.gr/posts/the-benefits-of-the-hellenic-cadastre)  geospatial data,  namely its DSM and DEM.